Deep Reinforcement Learning

An implementation of position controllers for parallel robots based on Machine Learning

In this post I will be explaining one of the controllers that I implemented during my Internship (and Master’s Thesis) working with rehabilitation parallel robots. One of the objectives of this internship was to experiment with Artificial Intelligence techniques, to demonstrate that the control architecture implemented in ROS2 is modular enough to be able to train algorithms and use them.

The particular technique that I experimented with was Reinforcement Learning or Deep RL in case that Neural Networks with hidden layers are used for some policies. The basic idea of Reinforcement Learning can be seen in the following image:

PPO+PD Reward training.

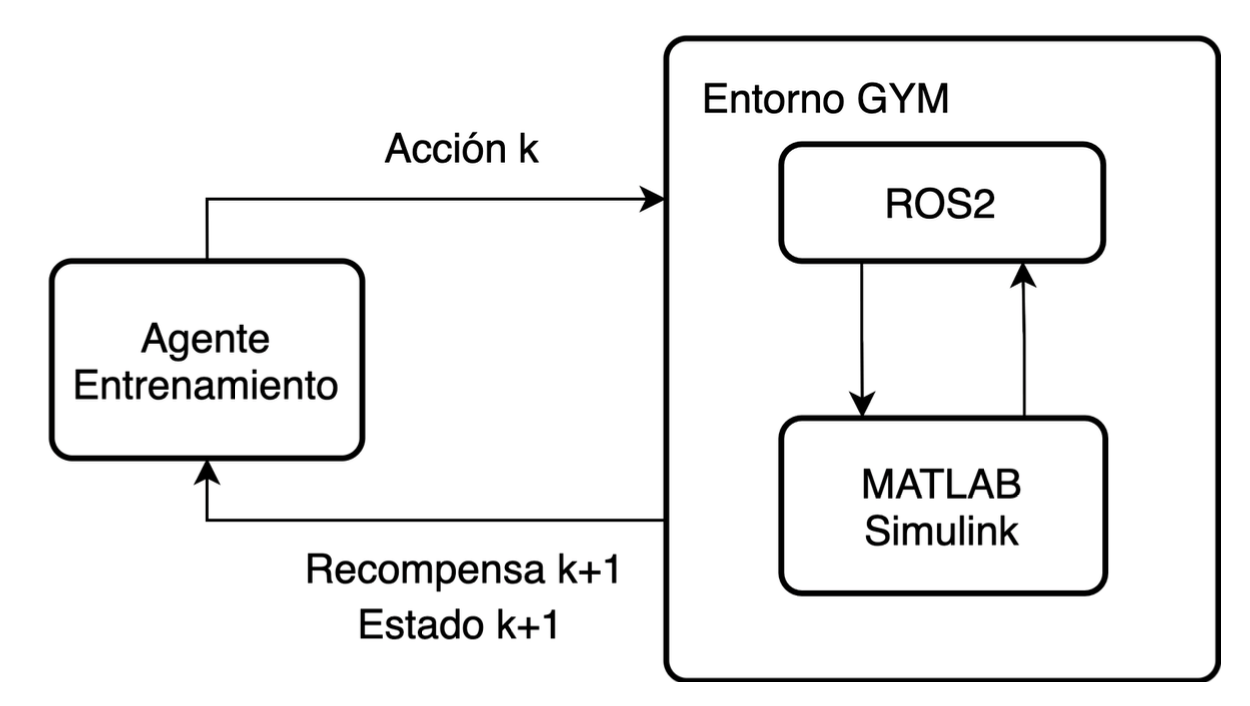
As the image shows, there is an agent that applies an action in a certain time step to the environment, this environment can be a real robot or a simulated one. After that, the environment will return a reward and a state of the robot. The agent will use this information to update its policy and apply a new action to the environment, which hopefully will maximize the obtained reward. Because the simulation of the parallel robots were implemented in Simulink, I created an interface between ROS2 and Simulink and then I created a gym environment that works on top of this and works as an interface to the agent. Thanks to this gym interface, many agents from different libraries can use this enviroment to train and use the algoritm to infer. The library that I decided to use was Stable Baselines, which implements the algorithms with Tensorflow.

I tried several approaches. I first noticed that it was difficult to train a policy to directly minimize the error between the desired position and the current position of the robot. The kinematics of parallel robots are complex and so the simulation where the robot can easily achieve a singular configuration. For this reason, I also did this work with the 3 DOF robot. Another thing is that Reinforcement Learning algorithms tend to be implemented on top of a lower level controller, which is based on standard control theory and that ensures stability. For this reason, I focused on a particular approach which is mentioned in some research papers:

  • Reinforcement Learning Based Compensation Methods for Robot Manipulators. Yudha P. Pane; Subramanya P. Nageshrao; Jens Kober; Robert Babuska. Engineering Applications of Artificial Intelligence, 2018
  • Residual Reinforcement Learning for Robot Control. Tobias Johannink, Shikhar Bahl; Ashvin Nair; Jianlan Luo; Avinash Kumar; Matthias Loskyll; Juan Aparicio Ojea; Eugen Solowjow; Sergey Levine. 2018.

The apprach I followed was to combine a PD controller with a Reinforcement Learning algorithm, so that the RL algorithm would learn to model errors caused by friction, gravity, dynamics, etc. I got the best results with the TRPO and PPO algorithms. Stable Baselines also provides logging info based on Tensorboard to monitor the training process. Here you can see some of the results (reward obtained in each step during training):

TRPO+PD Reward training.

PPO+PD Reward training.

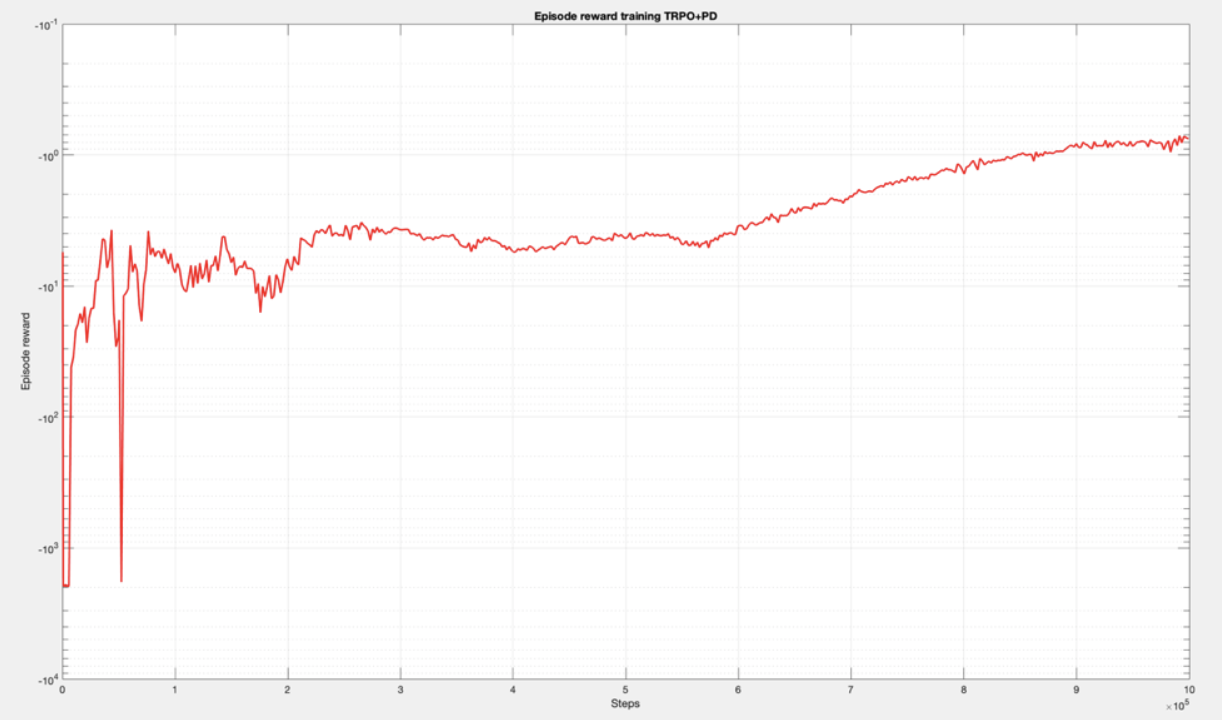
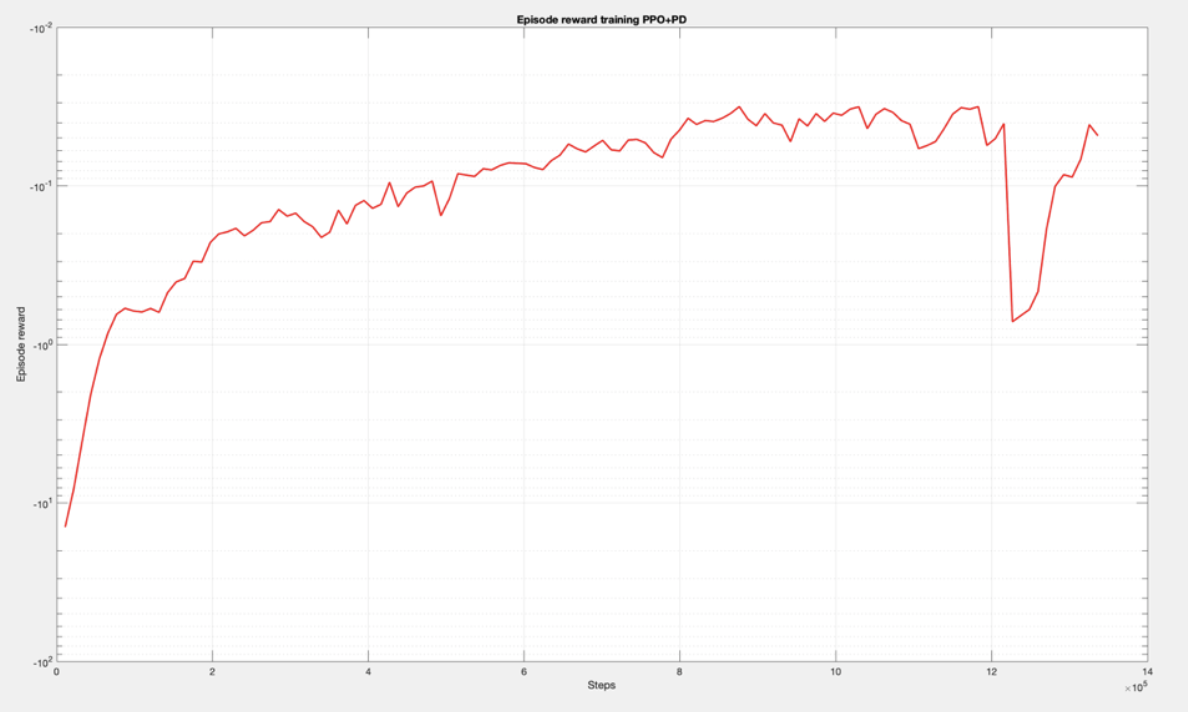
These algorithms were training with a dataset of a 100 different trajectories and evaluated afterwards with trajectories that were not used for training. Something very important in Reinforcement Learning is to define the Reward function. I experimented with several variations. When working with robots, it is not only important to minimize the position error, but also to have a smooth enough control action, something that is actually achievable by the physical actuators. This is why this reward function, which has a term to penalize the position error, but also the increment of the control action:

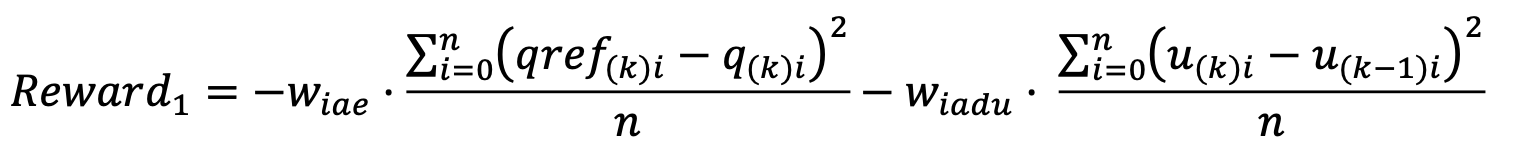
Reward function that penalises the position error and also the increment of the control actions with weights.

I also tried using a reward function, which rather than penalising the increment of the control action, it penalises the velocity error. However, this requires to have a good estimation of the velocity of joints of the robot.

Reward function that penalises the position error and also the velocity error with weights.

PPO+PD Desired trajectory versus measured in joint space.

PPO+PD Position error in joint space.

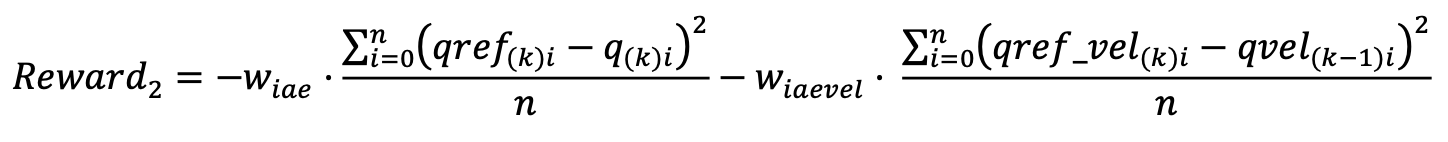
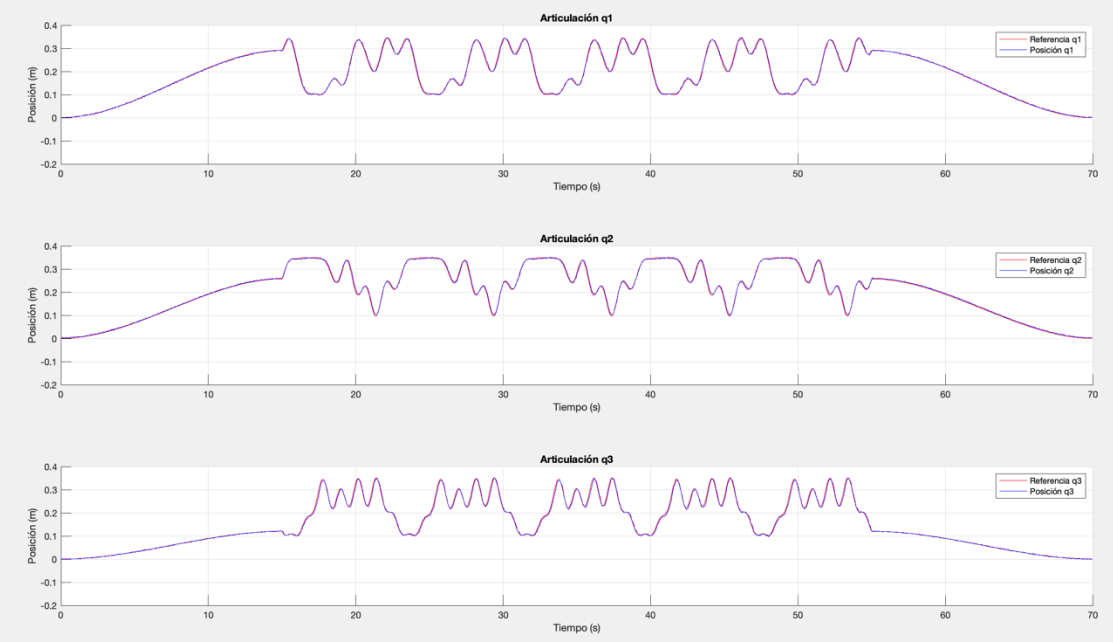
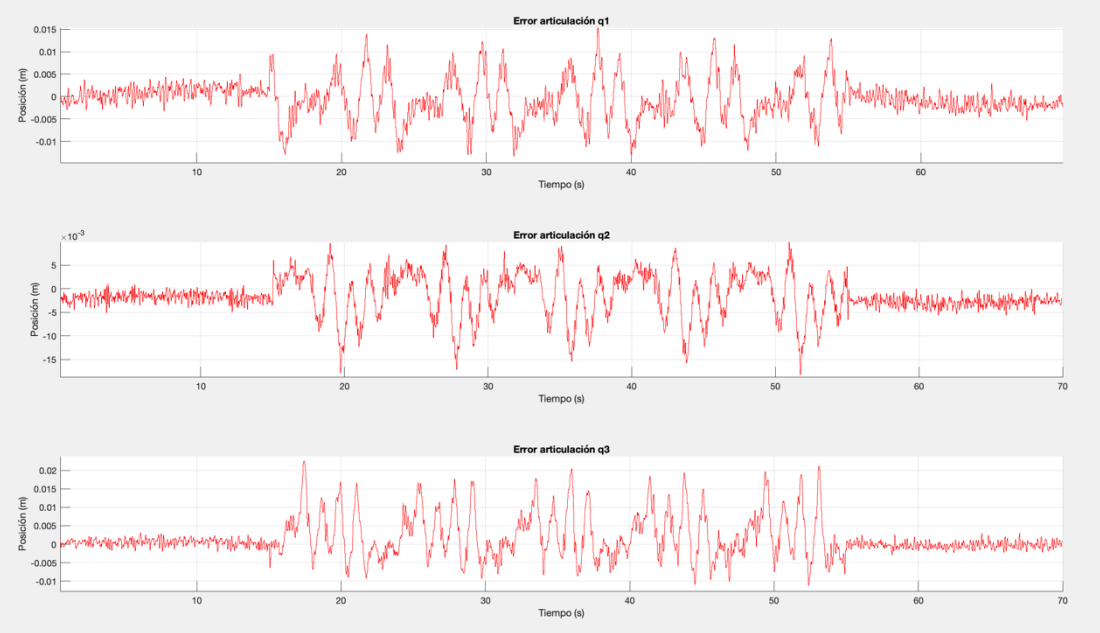
Something I noticed during the training is that the more the agent was training, the smaller the control action of the PD was produced. This is because the RL algorithm was learning to compensate the most important terms of the dynamics of the robot, which make smaller the position error and therefore smaller what the P term needs to output. For this reason, afte training, I decided to test the algorithm without the PD controller, and this was the result:

PPO without PD.

Finally, after studying the accumulation of the position error in each step for several trajectories, the RL+PD algorithm was able to improve this metric by 40% compared to the single PD controller.